Abstract
How can we explain the predictions of a black-box model? In this paper, we use influence functions — a classic technique from robust statistics — to trace a model’s prediction through the learning algorithm and back to its training data, thereby identifying training points most responsible for a given prediction. To scale up influence functions to modern machine learning settings, we develop a simple, efficient implementation that requires only oracle access to gradients and Hessian-vector products. We show that even on non-convex and non-differentiable models where the theory breaks down, approximations to influence functions can still provide valuable information. On linear models and convolutional neural networks, we demonstrate that influence functions are useful for multiple purposes: understanding model behavior, debugging models, detecting dataset errors, and even creating visually-indistinguishable training-set attacks.
블랙박스 모델의 예측을 어떻게 설명할까요?
본 논문에서는 고전적인 통계 기법을 사용하여 학습 알고리즘을 통해 얻어진 모델의 예측을 영향 함수를 사용하여 추적해보고, 주어진 예측을 주는 모델이 또다른 학습 데이터를 받았을 때 어떤 영향을 보이는지 알아본다.(즉 훈련 데이터에서 해당 데이터를 없앴을 때, 예측에 어떤 영향을 끼치는가?)
현대 머신러닝을 위한 영향함수의 확장을 위해서, 간단히 Hessian-vector 내적과 그래디언트를 요구하는 방법을 개발하였다.
학습에 부정적 영향을 끼치는 non-convex나 non-differentialble의 특성을 가지고 있는 모델이 여전히 가치있는 정보를 제공할 수 있음을 영향 함수를 통해 확인하였다.
선형 모델이나 컨볼루션 신경망에서 영향 함수가 다양한 목적에 있어 유용하다는 점을 증명하였다: 모델의 행동 이해, 모델 디버깅, 데이터셋 에러 감지, 시각적으로 구분 불가능한 훈련 세트의 에러.
요약
- 이 논문은 모델이 에측할 때, 대체 왜 그런 예측을 만들었는지에 대한 질문의 답변을 생각해본 논문이다.
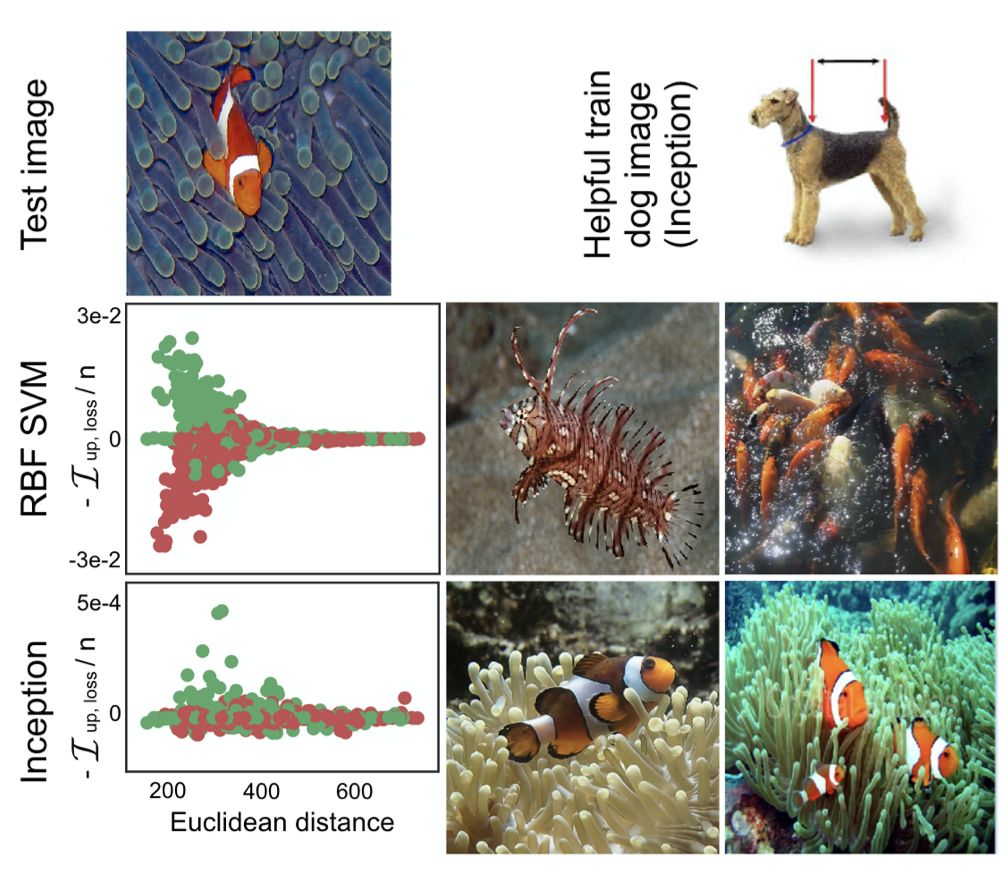
- 이 논문은 영향 함수를 사용하여 각 모델이 어떤 훈련 데이터에서 가장 영향을 받는지에 대한 예시를 밑의 그림에서 볼 수 있다. SVM은 픽셀단위에 예민함을 보이며, 예시 사진을 보면 주황색이 많이 들어간 사진들이 해당한다.(두 번째 행, 단순 주황색) 하지만 본 논문에서 사용된 Inception, 신경망의 경우는 표현을 학습하기 때문에 좀 더 복잡한 사진이 영향을 끼치는 것을 볼 수 있다.(세 번째 행, 주황색, 물고기 등)
- 논문에서는 모델 파라미터에 대한 영향력, loss에 대한 영향력, input space의 변화에 대한 영향력에 대해 설명한다.
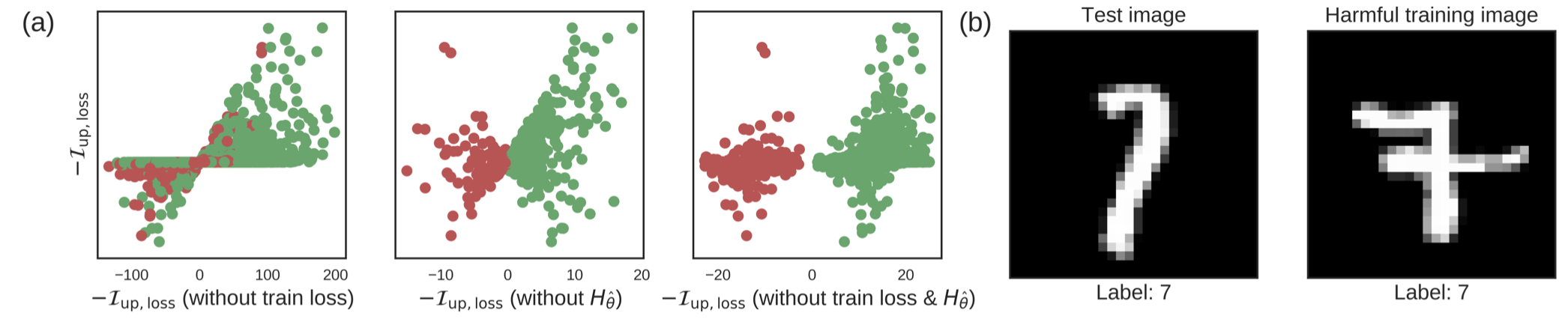
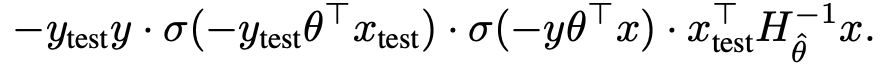
- 위의 예는 로지스틱 회귀에서 7과 1을 구분하는 문제이다. 초록색은 Training과 test가 7, 빨강색은 Training 1, test 7인 것을 의미한다. (a)는 각각 위의 식에서 train loss, Hessian, train_loss + Hessian을 빼본 것의 결과이다. (b)와 같은 경우는 테스트 이미지가 7일 때, 오른쪽 이미지를 7이라고 훈련시킨 경우에는 왼쪽 이미지를 예측하기가 힘들어진다는 것을 의미한다.
- Loss가 non-convex이면, quadratic loss로 가정하고 했더니 잘된다.
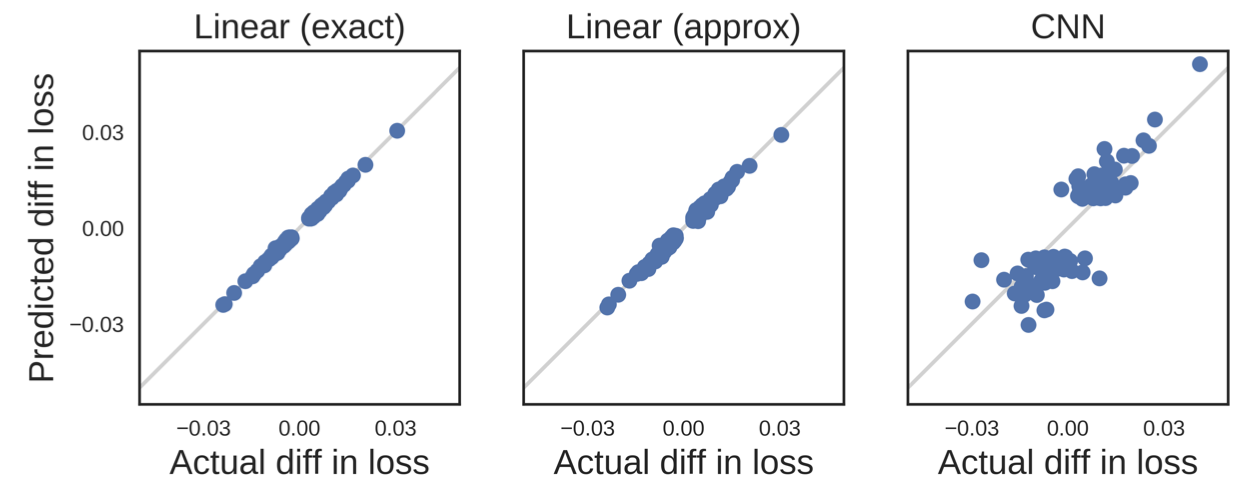
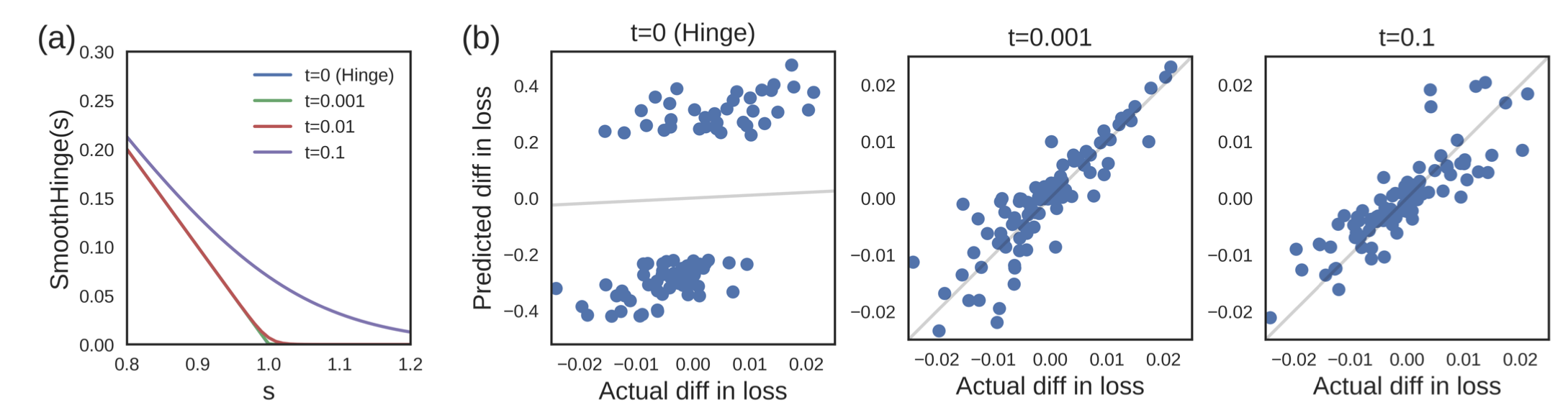
- Loss가 미분 불가능하면, 근사를 해서 미분 가능한 함수로 바꾸면 된다. 이 경우에는 대충 근사해도 잘되는 걸 확인할 수 있었다.
- 영향 함수는 각각의 훈련 데이터에 대한 영향을 알아볼 수 있으며, 도메인 미스매치를 디버깅할 수 있다. 또한, mislabel 문제에 대해서도 잡아낼 수 있는 장점이 있다.
Reference
Koh, P. W., & Liang, P. (2017, August). Understanding black-box predictions via influence functions. In Proceedings of the 34th International Conference on Machine Learning-Volume 70 (pp. 1885-1894). JMLR. org.
'# Paper Abstract Reading' 카테고리의 다른 글
| WaveNet - A Generative Model for Raw Audio (0) | 2019.12.07 |
|---|---|
| Learning to Remember Rare Events (0) | 2019.12.02 |
| Inception and Xception (0) | 2019.11.26 |
| PVANet: Lightweight Deep Neural Networks for Real-time Object Detection (0) | 2019.10.29 |
| Deep Visual-Semantic Alignments for Generating Image Descriptions (0) | 2019.10.28 |