KL-Divergence는 텐서플로우 공식 문서에 다음과 같이 구현되어 있습니다.
loss = y_true * log(y_true / y_pred)
의미는 다르지만 y_true / y_pred을 보니 분포를 비교할 때 사용하는 F-Distribution이 생각나기도 하네요.(그냥 여담)

KLD(이하 KL-Divergence)는 P 분포와 Q 분포가 얼마나 다른지를 측정하는 방법입니다. 여기서 통계적으로 P는 사후, Q는 사전분포를 의미합니다.

텐서플로우 공식 문서에 정의되어있는 용어로 설명해보면, KLD는 y_true(P)가 가지는 분포값과 y_pred(Q)가 가지는 분포값이 얼마나 다른지를 확인하는 방법입니다.
KLD는 값이 낮을수록 두 분포가 유사하다라고 해석합니다. 정보이론에서 흔히 볼 수 있는 엔트로피(Entropy) 또한, 값이 낮을수록 랜덤성이 낮다고 해석하는 것과 비슷합니다.
두 가지의 해석 방법이 비슷한 것은 바로 KLD에 크로스-엔트로피(Cross-Entropy) 개념이 이미 포함되어 있기 때문입니다.
KLD와 크로스 엔트로피
정보이론에서 정보량은 다음을 효과적으로 표현하기 위해 로그를 사용하여 표현합니다.
- 확률이 높을수록 → 매우 당연하게 일어날 사건
- 확률이 낮으면 → 자주 일어나지 않는 특별한 사건
또, 우리가 흔히 볼 수 있는 엔트로피는 평균 정보량을 나타내므로 다음과 같이 표현합니다.

예측할 수 있는 5개 상황이 각각 벌어질 확률을 [0.2, 0.2, 0.2, 0.2, 0.2]라고 가정했을 때, 엔트로피는 0.2 x 5 x log(0.2)가 되겠죠.
이제 KLD에 왜 Cross-Entropy가 포함되어 있는지 보겠습니다. 또, 편의를 위해 아래에서 볼 수 있는 p와 q를 다음과 같이 생각하겠습니다.
- p : 실제 세계에서 관찰하여 얻어낸 확률 ; 실제 확률분포 P
- q : 모델이 예측한 확률 ; 확률분포 P로 근사될 분포 Q

KLD 식을 다시 나누면 그림에서 왼쪽항처럼 나눌 수 있는데, 이는 분명 Entorpy - Entropy같아 보이지만, 맨 앞의 식에서 로그 안의 값이 모델이 예측한 확률 q를 나타내고 있기 때문에 Cross-Entropy - Entropy가 됩니다.
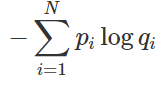
결과적으로 모델이 예측한 확률분포(Q)의 정보량과 실제 확률분포(P) 정보량의 차이를 계속 학습함으로써 Q를 P에 근사한다고 표현할 수 있습니다. 그래서 이에 대한 차이(정보량)를 분포가 유사한지에 대한 정도로 다시 해석할 수 있는 것입니다.
모델 학습에서의 KLD
우리가 보통 Classification 문제에서 Binary 또는 Categorical Cross-Entropy를 쓰는데, 사실 KLD를 사용하는 것과 동일하다고 표현해도 무방합니다.
위 식에서 Entropy에 해당하는 부분은 실제 값으로 고정된 값이기 때문에 (Loss 최소화에 영향을 주지 않아) 생략할 수 있고, 실제 모델이 학습하면서 최소화할 부분은 KLD 식의 앞부분에 해당하는 Cross-Entropy이기 때문이죠.
하지만 실제 진짜를 모방하기 위해 가짜의 분포를 정말 잘 만들어내야 하는 GAN에서는 이에 대한 정보가 굉장히 중요한 것 같습니다.
그래서 실제로 증명 과정에서 KLD를 사용하진 않고, KLD를 거리 개념으로 해석할 수 있게 변환한 Jensen-Shannon divergence를 사용합니다.

우리가 흔히 생각하는 거리는 A와 B를 보았을 때, 다음을 만족해야 합니다.
- A 기준에서 바라본 B까지의 거리 = B 기준에서 바라본 A까지의 거리
하지만 KLD는 KLD(P || Q) ≠ KLD(Q || P) 이기 때문에 거리로서 해석될 수 없습니다.
'# Machine Learning > 글 공부' 카테고리의 다른 글
| DeepSeek - R1 알고리즘 관련 글 (0) | 2025.02.08 |
|---|---|
| 이제 금융권에서는 딥러닝으로 고객을 분석합니다? (0) | 2020.11.23 |
| 추천 시스템(Recommendation System) 공부 정리 (1) (0) | 2020.09.16 |
| BERT 설명하기 (3) | 2020.08.07 |
| 클래스 불균형, UnderSampling & OverSampling (0) | 2019.09.06 |