여러분도 아시다시피 Set에서는 여러가지 정의가 있습니다.
set, element, subset, universal set(집합을 덮을 수 있는 전체 집합), set operations.
위의 개념들은 초등학교에서 배우는 것으로 누구나가 다 알 수 있는 사실입니다. 다음으로
- disjoint sets : A∩B = ∅
- partition of A : 부분 집합
- Cartesian product : 집합의 곱을 뜻합니다.
- example) A = {1, 2}, B = {3, 4, 5}
- A * B = {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5)}
- power set : 집합 A의 모든 부분 집합을 뜻합니다 -> 2^A
- cardinality A : finite, infinite, countable, uncountable, denumerable(countably infinite)
- 쉽게 카디널리티는, 차원이라고 생각하면 조금 쉬울 수도 있습니다.
- 집합(cardinality)에서 A(m), B(n)이라면 AB는 (mn)의 cardinality를 가지게 됩니다.
- 두개의 집합이 one-to-one이라면, 두 집합의 cardinality는 같습니다.
- countable : 예를 들어, 자연수의 집합(1,2,3,4 ....) 과 어떤 집합이 one-to-one 대응이 된다면 그를 countable (infinite)라고 부르게 됩니다.
- 예를 들면, 정수들의 집합과 분수들의 집합은 countable이다. 둘은 자연수의 집합과 one-to-one대응이 되기 댸문이죠.
- 그렇다면 정수는 양수만 있는게 아니라 음수만 있는데 그게 어떻게 되냐? 라고 물어 보실 수 있는데요. 이 부분은 무한대에서 2를 곱하면 똑같이 무한대죠? 똑같은 개념입니다.
그래서 이처럼 셀 수 있는 무한대의 집합을 denumerable이라고 부릅니다. 또한 이를, 수학적으로 aleph null이라고 부릅니다.
not countable한 것을 uncountable 이라고 합니다. 한마디로 셀 수 없는 무한 집합입니다. 또한 수학적으로 countinuum이라고 표현하빈다.
이를 설명할 때에는 대표적인 예시가 있습니다.
Q : 0과 1사이의 집합이 몇개 일까요?
A : 무한개요.
위의 답변이 이해가 가시나요? 당연한 얘기입니다. 그렇다면
Q : 0과 1사이의 집합과 정수에서의 집합은 둘 다 같은 무한대인가요?
네! 답은 '아니오' 입니다. 이를 증명한게 Cantor라는 수학자입니다. 이를 증명하는 과정은
C = [0, 1]
- C를 countable이라 가정
- C에 대응하는 시퀀스, S가 존재한다고 가정
- 우리가 0과 1사이의 숫자를 다루기 때문에 다음과 같이 표현할 수 있습니다.
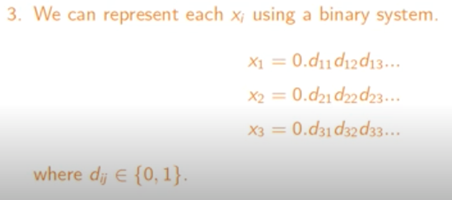
이와 같이 이진법으로 표현할 수 있습니다.
(시퀀스 S에 포함되는) x와 같이 표현하다 보면, 0과 1사이를 모두 표현할 수 있기때문에 countable하다는 것을 알 수 있습니다.
그런데 여기서 d = 1-d를 이용해서 하나씩 바꿔서 만든 x를 생각해 봅시다. 근데 이 새로 생긴 x는 S에 속하나요?
아니요. 0과 1을 바꿔서 만든 새로운 변수이기 때문에 S에 속하지 않고, C에 속하게 됩니다.
이를 이용하여 모든 x를 바꿔가면서 생각해보면, 일부의 x가 아닌 모든 x에 대해서 생각을 하기 떄문에, 이를 uncountable이라고 표현할 수 있게 됩니다.
- function or mapping f : U -> V
- domain U, codomain V (input, output이라고 생각하세요)
- image f(A) : A는 원소를 얘기하는 겁니다.
- range f(U)
사실 그래서 많은 machine learning 에서 푸는 문제가 preimage의 형태입니다.
어떠한 label을 가지고 개와 고양이를 train한 문제를 가지고 있을 때, 또 다른 data set, 즉 test set으로 이게 개인지 고양이인지를 파별해야하기 때문이죠.
마지막으로,
- one-to-one or injective : f(a) = f(b) -> a = b
- onto or injective : f(U) = V
- invertible : one-to-one and onto
설명은 그림을 보시면 잘 이해 되실겁니다!
Reference
edwith 강의, 최성준님
'# 기타 공부한 것들 > math' 카테고리의 다른 글
| posterior과 bayesian (6) | 2018.10.20 |
|---|---|
| Measure theory (1) | 2018.07.26 |
| Local Minimum, Local Maximum (0) | 2018.06.21 |
| Convexity(2) (3) | 2018.06.20 |
| Convexity(1) (4) | 2018.06.20 |











